Discovery of dynamical system models from data: Sparse-model selection for biology
Inferring causal interactions between biological species in nonlinear dynamical networks is a much-pursued problem across biological length scales, from gene regulation [1] to ecosystems [2]. Recently, sparse optimization methods have recovered dynamics in the form of human-interpretable ordinary differential equations from time-series data and a library of possible terms [3], [4]. These methods allow an efficient search through model space, assuming only a small subset of interactions determine behavior. The assumption of sparsity/parsimony is enforced during optimization by penalizing the number or magnitude of the terms in the dynamical systems models using L1 regularization or iterative thresholding. While successful and powerful, methods fail when only a subset of the state variables in the system are measured directly because of a decrease in the identifiability of the library terms decreases substantially, reducing the ability to determine the most likely model from data uniquely. Ultimately, we want to develop and use such methods to generate novel scientific hypotheses using an iterative experimental design framework (Fig. 1). To overcome the challenge of unmeasured states, we developed a new method using a variational annealing approach with sparse regularization and demonstrated recovery of model structure for chaotic systems when 2 out of 3 variables are measured [5]. Using this method, we generated novel models and hypotheses about body-temperature regulation in a hibernating ground squirrel, which has oscillatory dynamics (Result). Many of the models we recover cannot be distinguished given the data; they are members of a symmetry class of models that are unidentifiable. We are studying the structure of these symmetries using techniques from algebraic differential geometry [6] and working to redefine the cost function and optimization strategy to work well for these types of problems (Ongoing work).
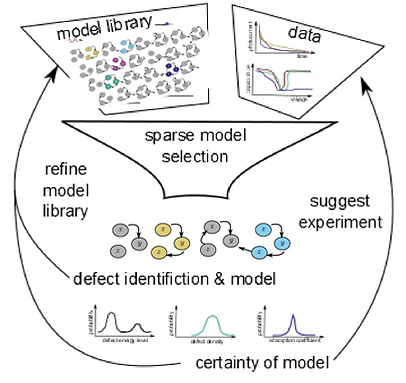
Figure 1. Schematic of sparse-model selection framework
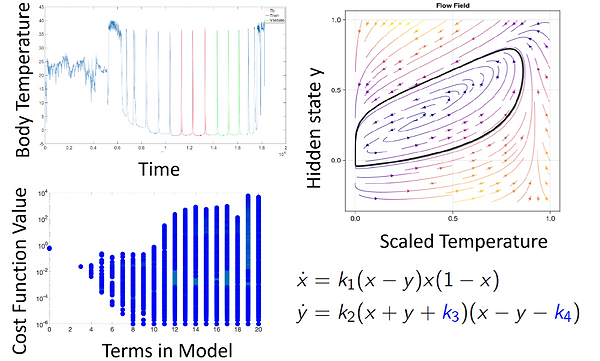
Figure 2. Model selection for metabolic regulation in hibernating mammal; Time-series data, Pareto Front of sparsely-selected models, one model's dynamics and structure.
Result: Using sparse-model selection to generate novel models for metabolic regulation in hibernating mammals. Cody Fitzgerald, an NSF-Simons Fellow in the Center for Quantitative Biology now funded in part by NITMB, and Andrew Engedal, an undergraduate researcher who is part of the QBREU program, applied our nonlinear sparse-optimization strategy to time-series data of body temperature of an arctic ground squirrel [7]. Notably, the animals can freeze their bodies at -4 degrees Celsius and periodically warm up during hibernation. The ground squirrel likely regulates these temperature spikes through metabolic control. A wide variety of model structures are recovered by varying the sparse threshold during optimization. The most parsimonious of these (low-cost function, sparse set of terms) have dynamical features that could cause the oscillatory spiking behavior seen in the data (Fig 2). Frequently, the optimization removes small terms that are needed to destabilize an attractive fixed point near zeros, and we currently add these manually but are pursuing ways to augment the sparsity thresholding or optimization to better enforce global oscillatory behavior. These adjustments may require the integration of dynamical systems theory into the optimization framework. Some of the models we have found are particularly appealing, in that they have terms that look like logistic growth or dynamics that match previously qualitatively described biological hypotheses. In particular, many models have an internal state that, when it falls below a threshold, causes the body temperature to spike back up. This behavior is consistent with the “depleted metabolite hypothesis” where the organism uses a decaying metabolite as a time-keeping mechanism to warm up periodically and replenish the metabolite, but until now, no dynamical systems model have been proposed. Our results propose several possible model structures which may have different biological interpretations.
Ongoing work: Studying the geometry of sparse-optimization cost functions for dynamical systems to improve the characterization of likely models. Christina Catlett, a graduate student funded in part by NITMB and Alasdair Hastewell, an NITMB Fellow, are studying the relationship between experimental measurements, dynamical systems, and sparse-optimization. Christina has preliminary results showing that she can optimize sub-sampling of the data to improve the conditioning of the function library of model-selection problem, when all states are measured and the problem is linear. Improving the conditioning of the linear regression problem, in this case, should improve recovery rates for models. We hope to expand these sub-sampling optimization methods to systems with hidden variables. To understand the geometric structure of the cost functions that arise in model selection with hidden variables, Alasdair has been using differential algebraic methods to analyze the identifiability issues in the model library. He has also visualized the cost functions using methods from ML [8], [9] and found that unstable dynamical systems sampled during optimization can produce dramatic changes in the cost function near optimal solutions, making the cost functions difficult to navigate. We are working on strategies to avoid these issues and understand the interplay between sparsity, dynamical systems, and optimization.
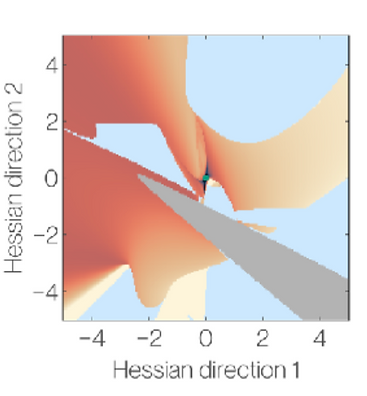
Figure 3 Visualization of cost function landscape using [8], [9]. Blue/grey are unstable.
References
[1] D. Marbach et al., “Wisdom of crowds for robust gene network inference,” Nat Methods, vol. 9, no. 8, pp. 796–804, 2012, doi: 10.1038/nmeth.2016.
[2] G. Sugihara et al., “Detecting causality in complex ecosystems,” Science (1979), vol. 338, no. 6106, pp. 496–500, 2012, doi: 10.1126/science.1227079.
[3] S. L. Brunton, J. L. Proctor, and J. N. Kutz, “Discovering governing equations from data: Sparse identification of nonlinear dynamical systems,” Proc Natl Acad Sci U S A, vol. 113, no. 15, pp. 1–31, Sep. 2015, doi: 10.1073/pnas.1517384113.
[4] N. M. Mangan, S. L. Brunton, J. L. Proctor, and J. N. Kutz, “Inferring biological networks by sparse identification of nonlinear dynamics,” IEEE Trans Mol Biol Multiscale Commun, vol. 2, no. 1, pp. 52--63, 2016, doi: 10.1109/TMBMC.2016.2633265.
[5] H. Ribera, S. Shirman, A. V. Nguyen, and N. M. Mangan, “Model selection of chaotic systems from data with hidden variables using sparse data assimilation,” Chaos, vol. 32, no. 6, Jun. 2022, doi: 10.1063/5.0066066.
[6] R. Dong, C. Goodbrake, H. A. Harrington, and G. Pogudin, “Differential elimination for dynamical models via projections with applications to structural identifiability,” SIAM J Appl Algebr Geom, vol. 7, no. 1, pp. 194–235, Nov. 2021, doi: 10.1137/22M1469067.
[7] H. E. Chmura, C. Duncan, G. Burrell, B. M. Barnes, C. L. Buck, and C. T. Williams, “Climate change is altering the physiology and phenology of an arctic hibernator,” Science (1979), vol. 380, no. 6647, pp. 846–849, 2023, doi: 10.1126/science.adf5341.
[8] M. P. Niroomand, L. Dicks, E. O. Pyzer-Knapp, L. Böttcher, and G. Wheeler, “Visualizing high-dimensional loss landscapes with Hessian directions,” Journal of Statistical Mechanics: Theory and Experiment, vol. 2024, no. 2, p. 023401, Feb. 2024, doi: 10.1088/1742-5468/AD13FC.
[9] H. Li, Z. Xu, G. Taylor, C. Studer, and T. Goldstein, “Visualizing the Loss Landscape of Neural Nets,” Adv Neural Inf Process Syst, vol. 31, 2018, Accessed: Sep. 16, 2024. [Online]. Available: https://github.com/tomgoldstein/loss-landscape